OVER
A taxa de “Over Night”, mais
comumente chamada de taxa de “over”, é a taxa de juros de um dia útil,
multiplicada por 30 (convenção de mercado, pois um mês tem 23 dias úteis). É
uma forma de expressar a taxa de juros muito usada no mercado financeiro, mais
especificamente no mercado aberto (open market)
Muitos produtos do mercado tem sua rentabilidade ou custo expresso na taxa de OVER (exemplo, CDI, HOT MONEY).
Toda taxa nominal “over’ deve
informar o número de dias úteis que os juros serão capitalizados de
forma que se possa apurar a taxa efetiva do período.
EXEMPLO
Suponha que a taxa “over” em determinado momento esteja definida em 5,4% a.m.. No período de referência da taxa, estão previstos 22 dias úteis. Qual a taxa efetiva do período?
Solução
Como a taxa “over” é geralmente definida por juros simples (taxa
nominal), a taxa diária atinge:
![]() ao dia .........taxa
nominal
ao dia .........taxa
nominal
Sabendo que no período de referência dessa taxa existem 22 dias úteis, a taxa efetiva é obtida
pela capacitação composta, ou seja:
i = (1 + 0,0018)22
– 1 = 4,04% a.m.
Em outras palavras, pode-se concluir que
4,04% representam a taxa efetiva para 22 dias úteis, ou mesmo para os 30 dias
corridos do mês.
Em resumo, os procedimentos de
apurar a taxa efetiva dada uma taxa nominal de juros “over” são os seguintes:
- Dividir a taxa de
“over” geralmente mensal, pelo número de dias corridos no período para se
obter a taxa nominal diária;
- Capitalizar a taxa
diária pelo número de dias úteis previsto na operação.
A
expressão básica de cálculo da taxa efetiva é:
![]()
sendo: “over” a taxa nominal mensal “over”, du o número de dias úteis previsto no prazo da operação.
Por outro lado, muitas vezes é interessante transformar uma taxa efetiva em taxa de “over”. No exemplo acima, foi definida uma taxa nominal “over” de 5,4% a.m. para um período com 22 dias úteis. Com isso, calculou-se a taxa efetiva de 4,04% a.m..
Se fosse dada a taxa efetiva para se transformar em “over”, o procedimento de cálculo seria o inverso, ou seja:
·
Descapitalizar
exponencialmente a taxa efetiva para cada dia útil previsto na operação;
·
Por
ser nominal, e definida mensalmente, a taxa “over” é obtida pelo produto da
taxa descapitalizada pelo número de dias corridos do mês.
Aplicando-se esses procedimentos na ilustração, tem-se:
i = 4,04% ao mês
du = 22 dias úteis
![]() = 0,18% ao dia útil
= 0,18% ao dia útil
OVER
= 0,18% x 30 = 5,4% a.m.
A formula de cálculo da taxa “over”, dada uma taxa efetiva de juros, pode ser desenvolvida da seguinte forma:
![]()
Substituindo os valores ilustrativos acima, chega-se
aos 5,4% a.m., ou seja:
![]() = 5,4% a.m.
= 5,4% a.m.
EXERCÍCIOS RESOLVIDOS
1. Uma taxa “over” está definida em 4,8% a.m.. Para um mês de 23 dias úteis, determinar a taxa efetiva
Solução
![]() = 3,75% a.m.
= 3,75% a.m.
2. Converter a taxa efetiva de 4,1% a.m. em taxa “over”, sabendo que no período existem 21 dias úteis.
Solução
![]() = 5,75% a.m.
= 5,75% a.m.
3. Uma aplicação pelo prazo de 35 dias corridos, que incluem 26 dias úteis, remunerou o capital aplicado a uma taxa “over” de 4,3% a.m. Determinar a taxa efetiva mensal de juros.
Solução
![]() ao dia.
ao dia.
Os juros são
capitalizados somente nos dias úteis. Os 25 dias úteis considerados na operação
equivalem a: 25/35 = 0,714286 dos 35 dias da aplicação financeira, ou a:
0,714286 x 30 = 21,42858 dias do mês. Logo:
![]() = 3,12% a.m.
= 3,12% a.m.
OPERAÇÕES FINANCEIRAS COM TAXA OVER
Ilustrativamente, suponha uma empresa
que obteve um empréstimo hot money por um dia.
A taxa de negociação contratada é nominal tipo “over” de 4,4% a.m., sendo
cobrado pelo banco, ainda, um spread (comissão) de 0,1% pela intermediação
da operação.
O spread é um percentual
cobrado pelo banco acima da taxa de negociação. É normalmente calculado para
cada renovação.
Sabe-se que, na prática, os encargos
dessas operações envolvendo taxa ‘over” são geralmente apurados por dia segundo
o critério de juros simples. O cálculo do custo efetivo processa-se:
OVER = 4,4% a.m.
OVER
= (4,4%/30) = 0,1467% ad.
Custo
efetivo do empréstimo incluindo o spread cobrado:
i
= [(1 + 0,001467)x(1 + 0,001)] – 1 = 0,247% ao dia
Logo, a taxa efetiva para todo o
mês, admitindo a existência de 21 dias úteis no período, e supondo também a
renovação do empréstimo 21 vezes no mês pela mesma taxa de juro (e de spread),
atinge:
i = [(1 + 0,001467)21
x (1 + 0,001)21] – 1 = 5,31% a.m.
Nessas condições, pode ser
estabelecida a seguinte expressão genérica de cálculo do custo efetivo final,
de uma operação de empréstimo, com taxa “over” e cobrança de spread:
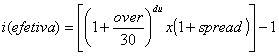
EXEMPLOS Ver ASSAF p. 168